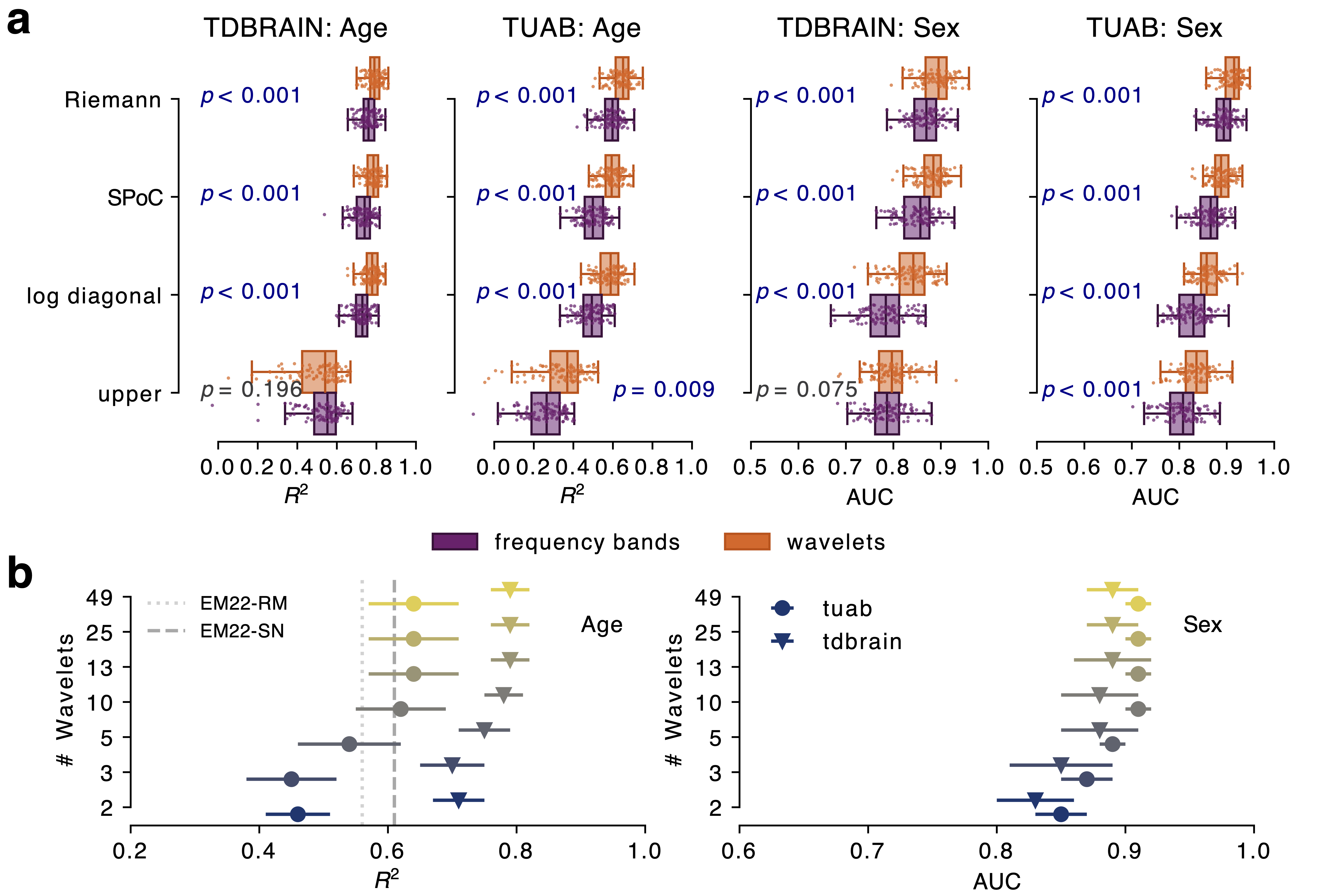
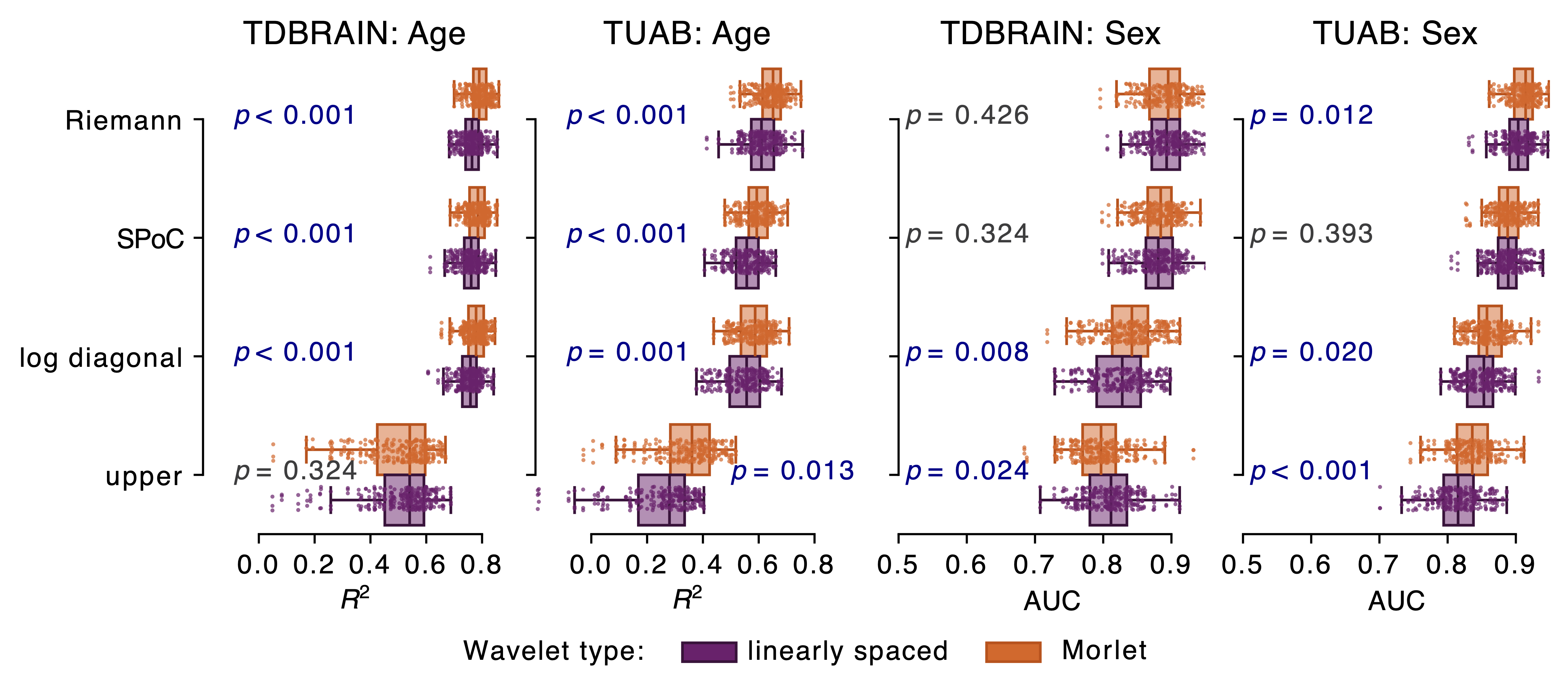
Forsyth, Anna, Rebecca McMillan, Doug Campbell, Gemma Malpas, Elizabeth Maxwell, Jamie Sleigh, Juergen Dukart, Joerg F Hipp, and Suresh D Muthukumaraswamy. 2018. “Comparison of Local Spectral Modulation, and Temporal Correlation, of Simultaneously Recorded EEG/fMRI Signals During Ketamine and Midazolam Sedation.” Psychopharmacology 235 (12): 3479–93.
Frohlich, Joel, Meghan T. Miller, Lynne M. Bird, Pilar Garces, Hannah Purtell, Marius C. Hoener, Benjamin D. Philpot, et al. 2019a.
“Electrophysiological Phenotype in Angelman Syndrome Differs Between Genotypes.” Biological Psychiatry.
https://doi.org/10.1016/j.biopsych.2019.01.008.
Frohlich, Joel, Meghan T Miller, Lynne M Bird, Pilar Garces, Hannah Purtell, Marius C Hoener, Benjamin D Philpot, et al. 2019b.
“Electrophysiological Phenotype in Angelman Syndrome Differs Between Genotypes.” Biological Psychiatry 85 (9): 752–59.
https://doi.org/10.1016/j.biopsych.2019.01.008.
———, et al. 2019c. “Electrophysiological Phenotype in Angelman Syndrome Differs Between Genotypes.” Biol. Psychiatry 85 (9): 752–59.
Görgen, Kai, Martin N Hebart, Carsten Allefeld, and John-Dylan Haynes. 2018. “The Same Analysis Approach: Practical Protection Against the Pitfalls of Novel Neuroimaging Analysis Methods.” Neuroimage 180 (Pt A): 19–30.
Hawellek, D J, P Garces, A H Meghdadi, S Waninger, A Smith, M Manchester, S A Schobel, and J F Hipp. 2022. “Changes in Brain Activity with Tominersen in Early-Manifest Huntington’s Disease.” Brain Commun 4 (3): fcac149.
Hipp, Joerg F, Joel Frohlich, Marius Keute, Wen-Hann Tan, and Lynne M Bird. 2021. “Electrophysiological Abnormalities in Angelman Syndrome Correlate with Symptom Severity.” Biol Psychiatry Glob Open Sci 1 (3): 201–9.
Hipp, Joerg F, David J Hawellek, Maurizio Corbetta, Markus Siegel, and Andreas K Engel. 2012. “Large-Scale Cortical Correlation Structure of Spontaneous Oscillatory Activity.” Nat. Neurosci. 15 (6): 884–90.
Hipp, Joerg F, Frederic Knoflach, Robert Comley, Theresa M Ballard, Michael Honer, Gerhard Trube, Rodolfo Gasser, et al. 2021. “Basmisanil, a Highly Selective GABAA-\(\alpha\)5 Negative Allosteric Modulator: Preclinical Pharmacology and Demonstration of Functional Target Engagement in Man.” Scientific Reports 11 (1): 7700.
Jochmann, Thomas, Marc S Seibel, Elisabeth Jochmann, Sheraz Khan, Matti S Hämäläinen, and Jens Haueisen. 2023. “Sex-Related Patterns in the Electroencephalogram and Their Relevance in Machine Learning Classifiers.” Hum. Brain Mapp., July.
Roy, Yannick, Hubert Banville, Isabela Albuquerque, Alexandre Gramfort, Tiago H Falk, and Jocelyn Faubert. 2019. “Deep Learning-Based Electroencephalography Analysis: A Systematic Review.” J. Neural Eng. 16 (5): 051001.
Sabbagh, D, P Ablin, G Varoquaux, A Gramfort, et al. 2019. “Manifold-Regression to Predict from MEG/EEG Brain Signals Without Source Modeling.” arXiv Preprint arXiv.
Sabbagh, David, Pierre Ablin, Gaël Varoquaux, Alexandre Gramfort, and Denis A Engemann. 2020. “Predictive Regression Modeling with MEG/EEG: From Source Power to Signals and Cognitive States.” Neuroimage 222 (November): 116893.
Schirrmeister, Robin Tibor, Jost Tobias Springenberg, Lukas Dominique Josef Fiederer, Martin Glasstetter, Katharina Eggensperger, Michael Tangermann, Frank Hutter, Wolfram Burgard, and Tonio Ball. 2017. “Deep Learning with Convolutional Neural Networks for EEG Decoding and Visualization.” Hum. Brain Mapp. 38 (11): 5391–5420.